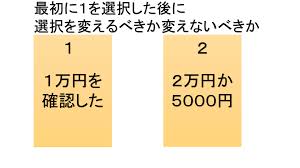
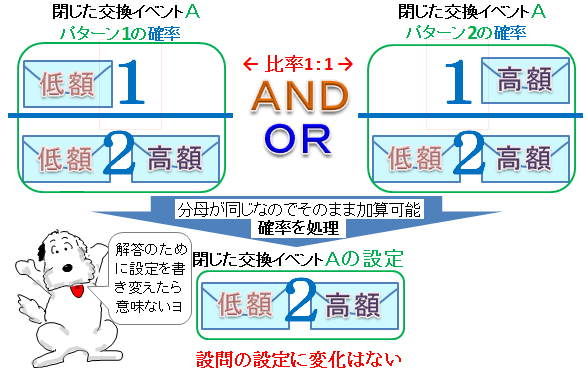
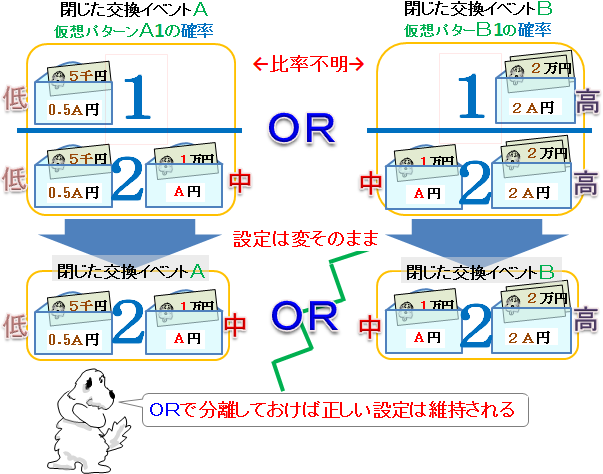
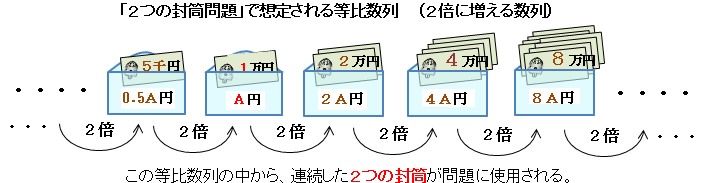
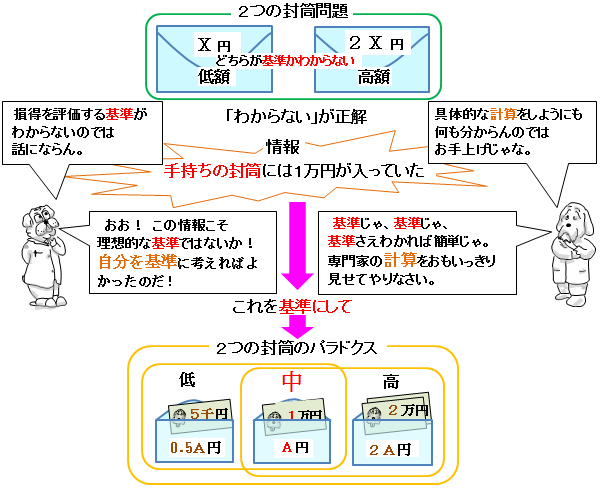
<問題> 手紙4通と封筒4枚があって、それぞれ1,2,3,4という番号がついている。同じ番号の手紙が、 同じ番号の封筒に入らないように、1通の手紙を1枚の封筒に入れる仕方は何通りか? <質問> 1→2→3→4→1のループ書籍 184ページの「2つの封筒・2」は、(数字を除けば)上記のお題その2と同じ問題である。 書籍では、期待値を計算して「替えた方がよい」と述べているが、間違いである。 混乱を避けるために、お題その2と同じく、金額は1万円として、追加で解説する。そもそも、「2つの封筒問題」では、はじめから終りまで一貫して封筒は2つしか存在しない。 たった 2つ の封筒の金額比をもって等比数列と呼べるかは別にして、問題を考えるために使った 3つ 以上の封筒の等比数列なんて、どこにも存在しない。

パラドックス モンティ問題 二つの封筒問題 Meet Me なにすればいいの
2つの封筒問題
2つの封筒問題-2つの封筒問題スレ 4 1 : 132人目の素数さん : (土) 問題 2つの封筒があり、中にそれぞれお金を入れる。 入っている金額の比は1:2とする。 選んで中を見ると円だった。 他方の封筒の金額の期待値は? この問題・類題に関する意見・質問のスレです。 このような問題を他スレで話題にしたりすると、高頻度で荒れる原因になりますので長形3号(n3) 1×235 jis 定形郵便。a4判ヨコ3つ折りが入る


モンティ ホール問題 好きのホームページ わかる二つの封筒問題
1 2つの封筒問題。 2つのうち片方にはある金額が入っていて、もうひとつには片方の金額の倍が入っています 2 「二つの2次方程式があり、一方の2解の間に、他方の1解が存在する」ことを証明する問題The two envelopes problem, also known as the exchange paradox, is a brain teaser, puzzle, or paradox in logic, probability, and recreational mathematics It is of special interest in decision theory, and for the Bayesian interpretation of probability theory Historically, it arose as a variant of the necktie paradox2つの封筒問題(パラドックス)を解説する情報の非対称性という魔物 2つの封筒問題とは次のような問題だ。 ここに2つの封筒がある。 一方には他方の2倍の金が小切手で入っている。 (わざわざ小切手と断ったのは封筒の中に1億円などが入る可能性を残すためだ。 ) あなたは適当に1つを選び、中身を見ると1万円が入っていた。 あなたの友人はもう1つを手に
Amazonで購入 ※「2封筒問題」をまだ知らない方は、「 2つの封筒問題:交換のパラドックスを解消する 」の「内容紹介」をご覧ください。 本書:「思考実験リアルゲーム」の、いわゆる「2封筒問題」の「正解」は、 〈最初に選んだ封筒の中身を確認した場合は、交換した場合の期待値は正しく、よって封筒を交換したほうが得である〉、というもので、 「 4 なぜホーム > 統計・データ解析 > 二封筒の問題:解決編? (二封筒の問題の続き) 問題を整理しよう。スワミは金額 $x$,$2x同書によると、この2封筒問題を扱うサイトや書籍は必ず炎上するらしく、出版界では密かに疎まれているんだそうです。Railsウォッチもついに炎上? 参考 数学 二封筒問題 参考 可能世界論 Wikipedia 同書で紹介されていた以下の本もちょっと気になります。
2つの封筒問題の日記 を念のためにもう少し丁寧に説明しなおしておく (深くなると、あとで思い出して検索するとき、めんどいねん)。 ついでだが、そこに貼っておいた Google Appsの表計算による シミュレーション (手抜き) 。 2つのパターンがある。 上がオリジナルの未開封型。 下が開封型。 2つの区別できない封筒があり、片方にはもう片方の倍の金額が入って二つの封筒問題(開封前) 二つの封筒問題はいくつもの錯覚によって、確率の間違いを起こしやすい問題です。 わかりやすくするために、少し問題を変えてみましょう。 AさんとBさんに、お金が入っている二つの封筒が配られました。 二つの封筒のうち、1つには二倍の金額が入っていることがお互いに告げられています。 開封前であれば、封筒の交換を何度でも「2つの封筒問題(封筒のパラドックス)」のトンチン解説 Type1:「期待値は正しい。交換した方が得」 梶谷通稔氏はビルゲイツの試験に受かるか? ~ 「スマート」な解き方?これが?


モンティ ホール問題 好きのホームページ わかる二つの封筒問題


2つの封筒問題を解析してみたヨ
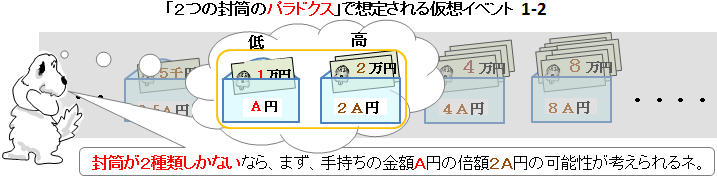
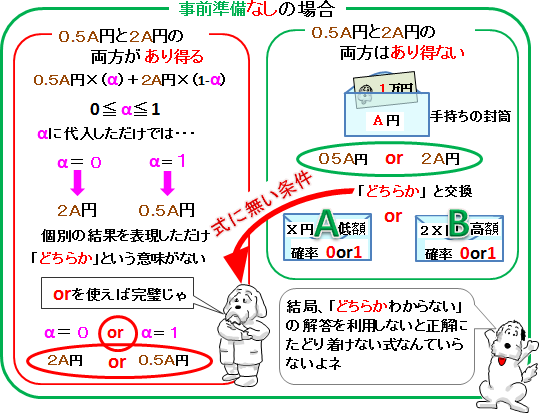
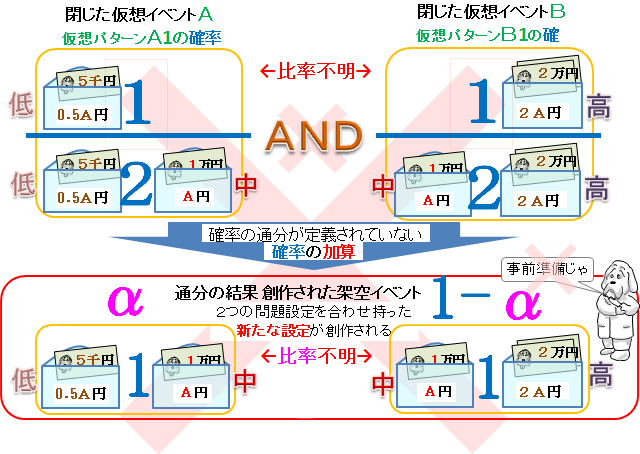
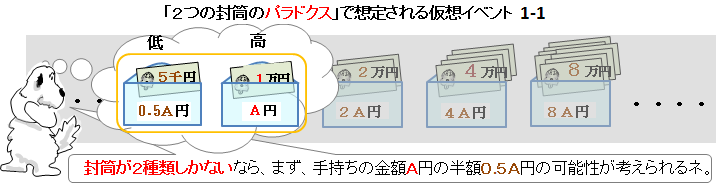
「2つの封筒問題」とは、 「ここに二つの封筒がある。 どちらかの封筒にはもう一方の2倍の金額が入っている。 今 あなたは一つの封筒を手にとった。 中を確認すると1万円が入っていた。長形2号(n2) 119×277 jis a4ヨコ3つ折・b5判タテ2つ折りが入る;2つの封筒問題について一般解を提供します。 (封筒のパラドックス) よく知られた2封筒問題とは、以下のような内容です。 2つの封筒があり、それぞれにお金が入っている。 一方の封筒に入っている金額が、他方の封筒に入っている金額の2倍であること



解説 思考実験での二つの封筒問題 Youtube


確率の期待値がよくわかる2つの封筒の問題とは
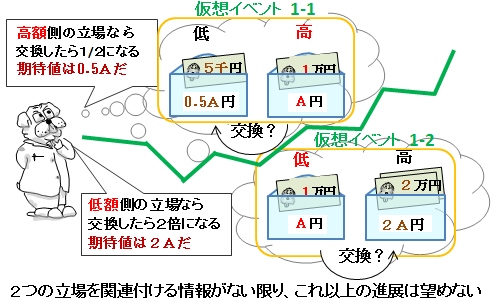
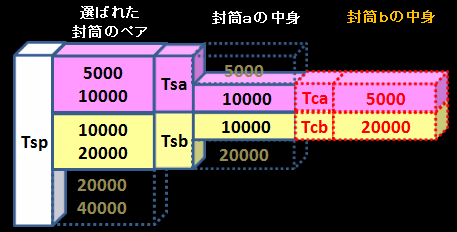
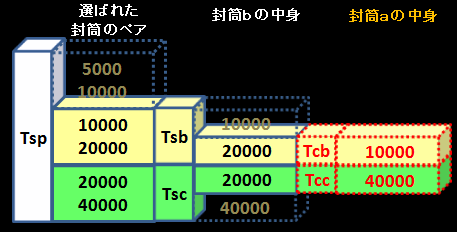
封筒を開けて10,000円を見たゲーム参加者にわかるのは、 胴元は、<5,000円、10,000円>のペアか<10,000円、,000円>のペアで お金を入れたということ、この2通りしかないという事実です。 そして、問題文を読む限りこの2通りに優劣はありません。7276円 パステルブルー 角2判がそのまま入るテープ付き封筒です。 業務用封筒 角2判がそのまま入るテープ付き封筒です。 業務用封筒 角2 テープ付 カラー封筒のり付き 角2封筒 角2 テープ付 紙厚100g500枚角型2号 紙厚100g500枚角型2号 角2封筒 日用品雑貨・文房具・手芸問題714 二つの封筒問題(問題516 の再掲) ゲームの主催者は, あなたに二つの封筒(ie, 封筒A と封筒B) から一つの封筒を選ぶチャンス を提供した 封筒A と封筒B にそれぞれV1 円とV2 円が入っている あなたには, 次が知ら されている (a) V1 V2 = 1=2 または, V1 V2 = 2


二つの封筒問題 非ベイジアン的方法


2つの封筒問題 交換のパラドックス その 期待できない 期待値 遅読猫の毛玉
切手問題とは、ある枚数の切手で作れない最小の金額(郵便料金)を求める数学の問題である 。 限られたスペース(封筒の面積)に切手を組み合わせて郵便料金を払う事ができるかを問う。 例えば、封筒は3枚の切手しか貼れず、使用可能な切手の額面が1円、2円、5円、円の場合、12円までの封筒問題の興味深いところは、封筒の中が100円だったらという一見中立的な仮定によって、条件が変化してしまうというところでしょう。 封筒の中身が100円だったということは、 50円の封筒と100円の封筒から100円の封筒を選んだ場合 100円の封筒と0円の封筒から100円の封筒を選んだ場合 の2PDF形式のファイルをご覧いただく場合には、Adobe Readerが必要です。 Adobe Readerをお持ちでない方は、バナーのリンク先から無料ダウンロードしてください。



パラレル 配られた二つの封筒問題 パラレルシフト 自分に還る人生のシフト



二つの封筒問題 ベイズアプローチ Landscapeの四季
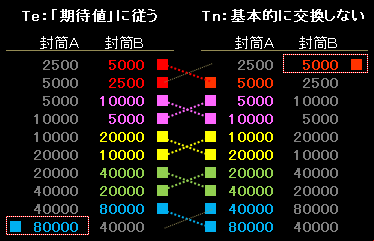
また、2封筒問題か。 この問題はプロの数学者の間でも一致した見解はない。 せいぜい、確率分布が決まっていないので計算できないと逃げるだけ。 ちなみに、現役の大学教授(数学)でも、Back 2つの封筒問題 続き・詳細・画像をみる 1 2 1名無しのコピペ 3 15年06月07日 0907 4 1ゲット 5 6 2名無しのコピペ12/26/17 · 2つの封筒問題 2つの封筒があり、一方の封筒に入っている金額はもう一方の封筒に入っている金額の2倍である。 一方の封筒を開けると100円入っていた。 あなたはそのままその100円をもらってもいいし、もう一方の封筒と交換することもできる そのまま



2つの封筒問題 交換のパラドックス その 期待できない 期待値 遅読猫の毛玉


二つの封筒問題 ベイズ統計学
問題516 二つの封筒問題 ゲームの主催者は,あなたに二つの封筒 (ie, 封筒Aと 封筒B)から一つの封筒を選ぶチャンスを提供した 封筒Aと 封筒Bにそれぞれ $V_1$円と$V_2$円が入っている あなたには,次が知らされている後編 (2つの封筒問題) YouTube 『ゆっくり解説』ゆっくりが確率のパラドックスについて解説! ! 後編 (2つの封筒問題) If playback doesn't begin shortly「二封筒問題」(Two envelopes problem) は「二つの封筒のパラドックス」( Two Envelope Paradox) とも呼ばれます。 しかしそのパラドックスは一つではありません。 ある人にとっては、 「交換した後の期待値が選んだ封筒の金額によらず交換する前の 125 倍であること」


モンティ ホール問題 好きのホームページ 二つの封筒問題のパラドックスたちとそのおまじない


2つの封筒のパラドクスの結論だヨ
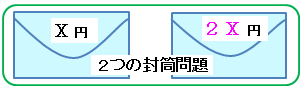
2.表示された「印刷」ダイアログで印刷する宛先を指定します 設定できたら印刷をクリックし、印刷を実行します <封筒の裏(うら)面に、差出人を印刷する場合> 1.メニューの裏面のみをク二封筒の問題 スワミ(ヒンズー教の坊さん)が,一つの封筒に x 円,もう一つの封筒に 2 x 円を入れ,一方をあなたに,もう一方を相手に渡した。 どちらの封筒を渡される確率も 1/2 である。 あなたが封筒を開けたら y 円入っていた。 相手の封筒の中身を Y とする。 あなたは考えた。 封筒は等確率で渡されたのだから,確率 1/2 で Y = y / 2 または Y = 2 y のはずだ長形:縦サイズが横サイズの2倍程度ある封筒 長形1号(n1) 142×332 旧jis(1964年版まで) a4たて2つ折・b4判ヨコ3つ折りが入る;



あなたは何個知ってますか 頭を鍛える面白いパラドックス11選 アタリマエ


2つの封筒のパラドクスの結論だヨ
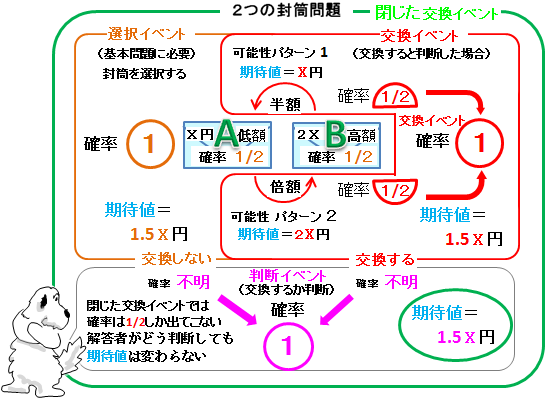
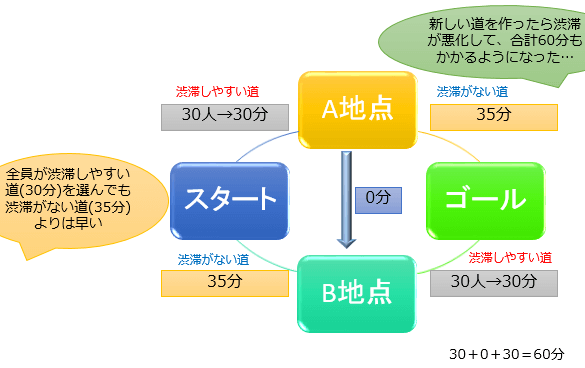
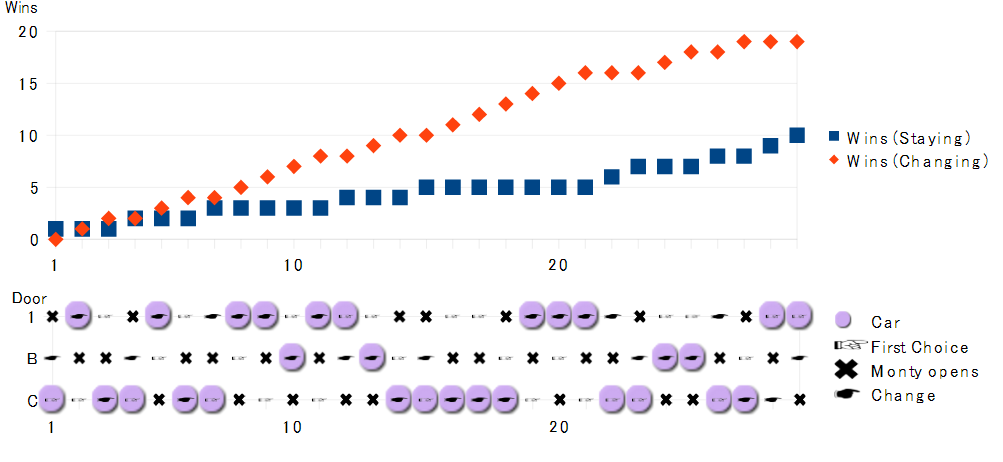
選択を変えるのか変えないのかと言う部分は、モンティ・ホール問題(選択を変えることによって正解率を上げることができる有名な確率の問題)と似ています。 選択を変えることで、確率が変わる問題が、「 2つの封筒 」の問題になります。 この問題は、期待値を金額と言った私たちになじみ易いことで例えることにより、とてもわかりやすく認識できます2つの封筒問題(two envelopes problem) 2)封筒を開けず金額を確かめる前なら、交換前後の金額の期待値 は同じだからどちらでもよい。 3)中に入ってる金額が一方が他方の4倍としか分からないが、基本問題 (a) プレイヤーに見た目区別がつかない封筒が二つ与えられる (b) 両方とも中には現金が入っているが額はわからない (c) 一方には他方の倍の現金が入っていることがわかっている (d) どちらかの封筒を一つだけ選んで中の現金をもらうことができる (e) 選んだ封筒を開ける前に他の封筒に変更できる (f) なるべく多くの金額を獲得したい


モンティ ホール問題 好きのホームページ 二つの封筒問題とモンティ ホール問題



2つの封筒問題を解析してみたヨ



二つの封筒問題 ベイズアプローチ Landscapeの四季


モンティ ホール問題 好きのホームページ 二つの封筒の錯覚から目覚めよ


モンティ ホール問題 好きのホームページ 二つの封筒問題の錯覚とスマリヤンの錯覚


Twitterで10万rtされた数学の問題がこちら 2つの封筒問題 不思議 Net


パラレル 配られた二つの封筒問題 パラレルシフト 自分に還る人生のシフト



あなたは何個知ってますか 頭を鍛える面白いパラドックス11選 アタリマエ



2つの封筒問題 交換のパラドックスを解消する 遅読猫 数学 Kindleストア Amazon


2つの封筒問題を解析してみたヨ



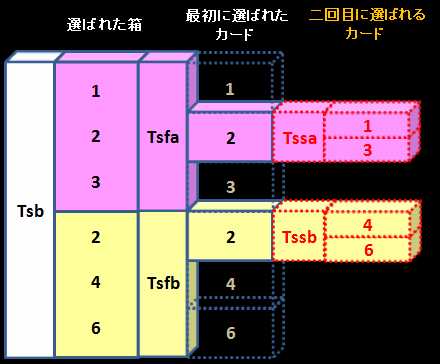
問題1は分かったのですが 問題2が分かりません 誰か説明お願いします Clear



2つの封筒問題 交換のパラドックス その 期待できない 期待値 遅読猫の毛玉


二つの封筒問題 パラドックス 株式投資に役立つ心理学


2つの封筒のパラドクスの結論だヨ


2つの封筒のパラドクスの結論だヨ


数学の中で有名な 2つの封筒のパラドックスがありますが あれは何がおかしい Yahoo 知恵袋


激論 ツイッターの封筒問題について 数学板 博士ちゃんねる


2つの封筒問題を解析してみたヨ



あなたは何個知ってますか 頭を鍛える面白いパラドックス11選 アタリマエ


あなたは何個知ってますか 頭を鍛える面白いパラドックス11選 アタリマエ



二つの封筒問題 ベイズアプローチ Landscapeの四季



二つの封筒問題 ベイズアプローチ Landscapeの四季



Amazon Co Jp 遅読猫 作品一覧 著者略歴


二つの封筒問題 ベイズ統計学



ゆっくり解説 ゆっくりが確率のパラドックスについて解説 後編 2つの封筒問題 Nicozon


モンティ ホール問題 好きのホームページ 二つの封筒問題の錯覚とスマリヤンの錯覚


二つの封筒問題 非ベイジアン的方法


2つの封筒問題 交換のパラドックス その 期待できない 期待値 遅読猫の毛玉



二つの封筒問題 ベイズアプローチ Landscapeの四季


二つの封筒問題 パラドックス 株式投資に役立つ心理学



メルカリ 5教科静岡県立高校入試模擬テスト 活用プラス問題 国数 参考書 1 000 中古や未使用のフリマ


二つの封筒問題 パラドックス 株式投資に役立つ心理学


2つの封筒問題 交換のパラドックス その 期待できない 期待値 遅読猫の毛玉


モンティ ホール問題 好きのホームページ わかる二つの封筒問題



Nupsc招待講演 アルゴリズムで広がる世界


モンティ ホール問題 好きのホームページ わかる二つの封筒問題



2つの封筒問題 交換のパラドックス その 期待できない 期待値 遅読猫の毛玉


あなたは何個知ってますか 頭を鍛える面白いパラドックス11選 アタリマエ



Futatsunofutomondaifutonoparadokkusuwokaisyousuru By Chidokuneko



2つの封筒の問題またはネクタイのパラドックス



Futatsunofutomondaifutonoparadokkusuwokaisyousuru By Chidokuneko



Rusl 2つの封筒問題 これわかんなかったら中学生以下の学力www 解答 T Co L7vanrethg 周りのやつアホすぎワロタw 拡散希望 T Co 9shgwepd R Y72


モンティ ホール問題 好きのホームページ 二つの封筒問題とモンティ ホール問題


2つの封筒問題を解析してみたヨ



2つの封筒問題 交換のパラドックスを解消する 遅読猫 数学 Kindleストア Amazon


二つの封筒問題 パラドックス 株式投資に役立つ心理学


パラドックス モンティ問題 二つの封筒問題 Meet Me なにすればいいの


モンティ ホール問題 好きのホームページ わかる二つの封筒問題


モンティ ホール問題 好きのホームページ 二つの封筒問題の錯覚とスマリヤンの錯覚


2つの封筒のパラドクスの結論だヨ



数学の話題 八起数学塾 大人のための数学塾 ネット受講可能



パラレル 配られた二つの封筒問題 パラレルシフト 自分に還る人生のシフト


2つの封筒問題を解析してみたヨ



未分類 理系の科学哲学 コペンハーゲン解釈 理系の西洋哲学史



パラドックス モンティ問題 二つの封筒問題 Meet Me なにすればいいの


モンティ ホール問題 好きのホームページ 二つの封筒の錯覚から目覚めよ



2つの封筒問題 交換のパラドックスを解消する 遅読猫 数学 Kindleストア Amazon


2つの封筒問題 交換のパラドックス その 期待できない 期待値 遅読猫の毛玉



Haruhiko Okumura 二封筒の問題 交換のパラドックス T Co Mwz3eiuqfo
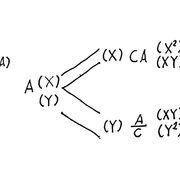


記事一覧 同額の大小は 残りの方が別の組で 規模の違う減増分は同期待値



2つの封筒問題は 見た後の大小は 同額なので 組が異る場合


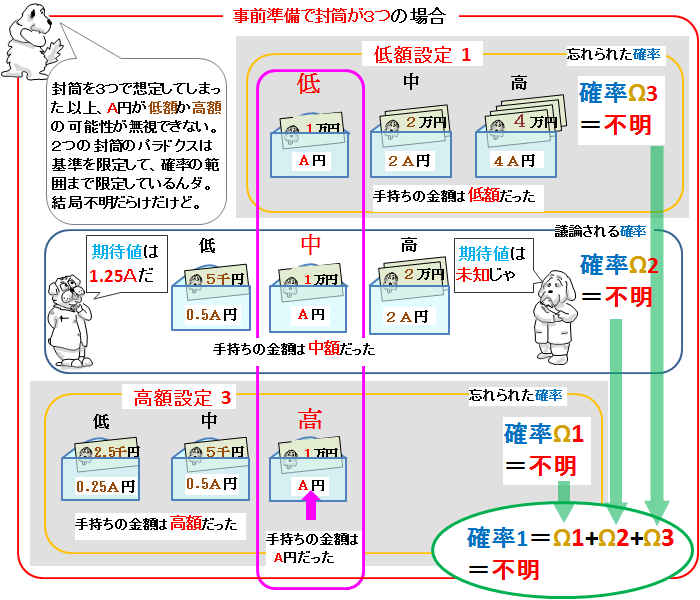
あなたは何個知ってますか 頭を鍛える面白いパラドックス11選 アタリマエ


2つの封筒のパラドクスの結論だヨ



2つの封筒問題 交換のパラドックス その 期待できない 期待値 遅読猫の毛玉
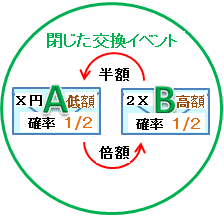


2つの封筒のパラドクスの結論だヨ


三つの中から賞金入りの封筒を選ばせ司会者は外れを1つ飛ばし残り Yahoo 知恵袋
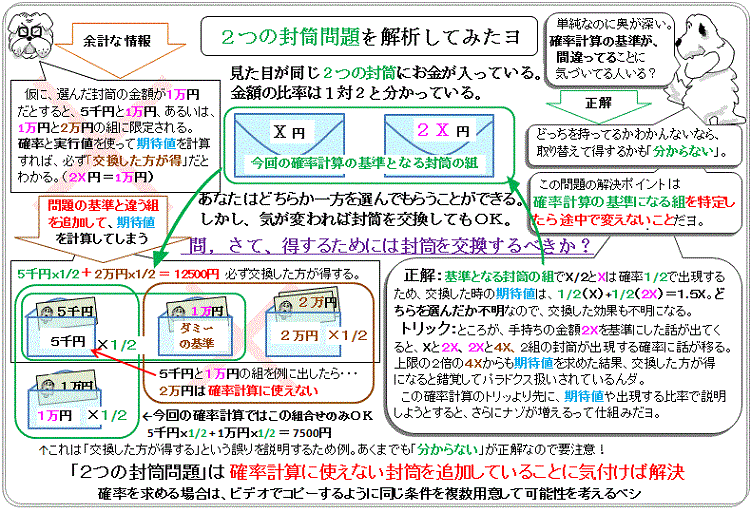


2つの封筒問題を解析してみたヨ
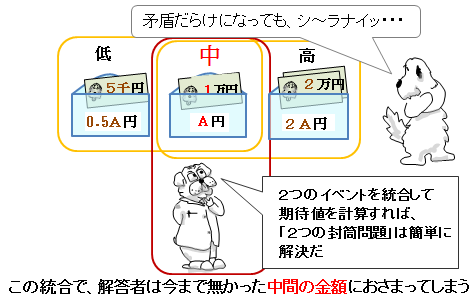


2つの封筒問題を解析してみたヨ



パラレル 配られた二つの封筒問題 パラレルシフト 自分に還る人生のシフト



二つの封筒問題 ベイズアプローチ Landscapeの四季


2つの封筒問題を解析してみたヨ


二つの封筒の問題ー確率と現実 Shinzorの日記
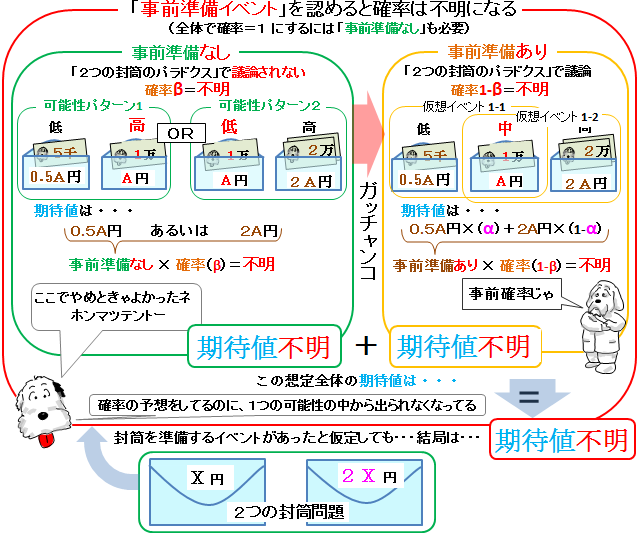


2つの封筒のパラドクスの結論だヨ


二つの封筒問題 非ベイジアン的方法


ゆっくり解説 ゆっくりが確率のパラドックスについて解説 後編 2つの封筒問題 ニコニコ動画



パラドックス モンティ問題 二つの封筒問題 Meet Me なにすればいいの


2封筒問題のなぞ すべての夢のたび


サンクトペテルブルクの二つの封筒問題
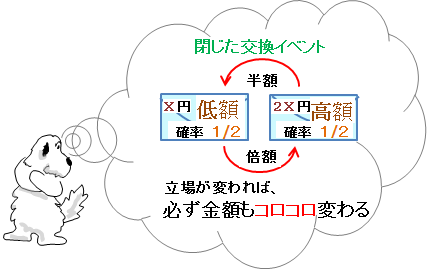


2つの封筒のパラドクスの結論だヨ


2つの封筒のパラドクスの結論だヨ


モンティ ホール問題 好きのホームページ 二つの封筒問題の錯覚とスマリヤンの錯覚


モンティ ホール問題 好きのホームページ 二つの封筒問題の錯覚とスマリヤンの錯覚


二つの封筒問題 非ベイジアン的方法


0 件のコメント:
コメントを投稿